Order and symmetry
There is a quote by the famous mathematician Carl Friedrich Gauss (1777-1855) – “The enchanting charms of this sublime science reveal themselves in all their beauty to those who look deeper”
The words “Think deeply about simple things” are also often quoted.
In the sections that follow, we look deeper into the 9×9 number layout. Interestingly, we discover patterns and symmetry that are noteworthy.
Students learn by number, position and colour. Symmetry can later be introduced as a mathematical surprise.
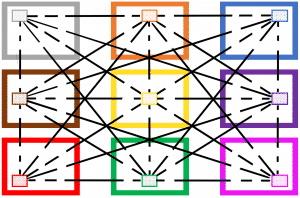
Square numbers - Symmetry and geometry
A square is the result of multiplying a number by itself.
- 1×1=1²=1
- 2×2=2²=4
- 3×3=3²=9
- 4×4=4²=16
- 5×5=5²=25
- 6×6=6²=36
- 7×7=7²=49
- 8×8=8²=64
- 9×9=9²=81
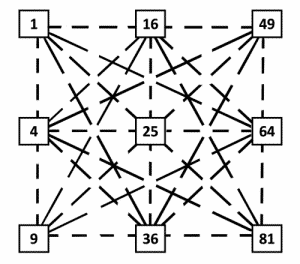
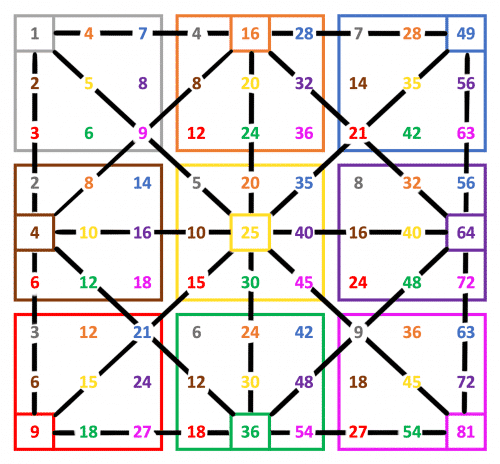
Remarkably, these square calculations are located in positions of symmetry. (8×2 and 9×4 are not square operations.)

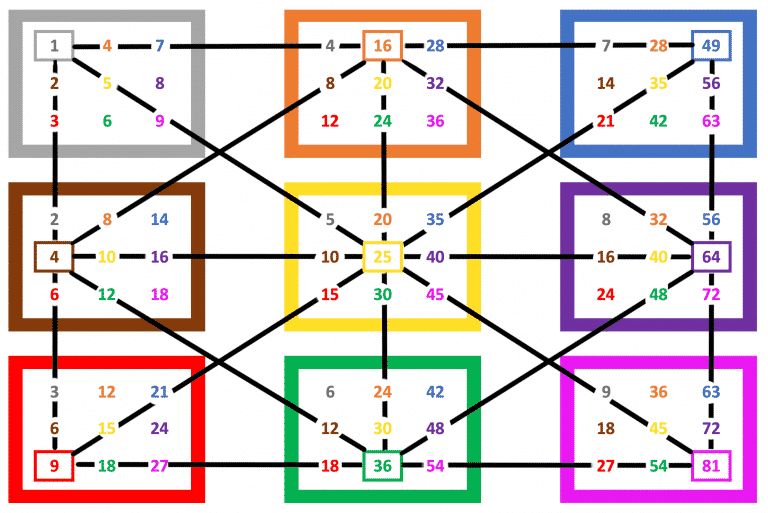
Connecting square numbers
If we connect any two square operations, symmetry in numbers exists on each connecting ray.
Between two adjacent squares “a²” and “b²“, the numbers “a x b” and “b x a” are symmetrically positioned about a middle number.
a=√a²
b=√b²
a x b = b x a
a x b and b x a are on the connecting ray between a² and b².
Also √(a² x b²) = a x b = b x a
For instance, if we connect square numbers 4²=16 (orange) and 8²=64 (purple), the number 32 appears twice on the line. Then, 4×8(purple) and 8×4(orange) are in symmetrical positions about a middle number 21 (7×3 (red)). Here √(16×64) = √1024 = 32.
Similarly, if we connect square numbers 2²=4 (brown) and 6²=36 (green), the number 12 appears twice on the line. Again, 2×6 (green) and 6×2 (brown) are in symmetrical positions about the middle number 21 (3×7 (blue)). Here √(4×36) = √144 = 12.
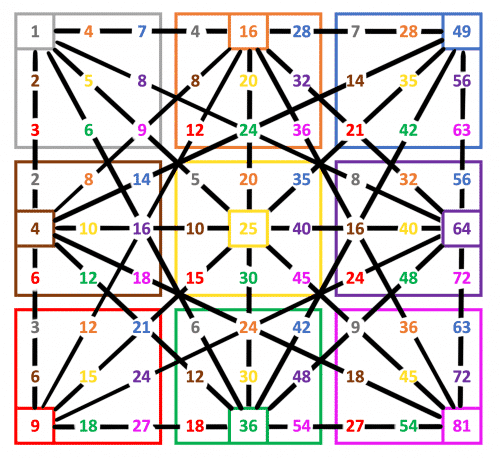
Rectangle
If we plot the numbers in a rectangle formation, some middle numbers are offset and the picture becomes less cluttered. Symmetry of “a x b” and “b x a” remains.
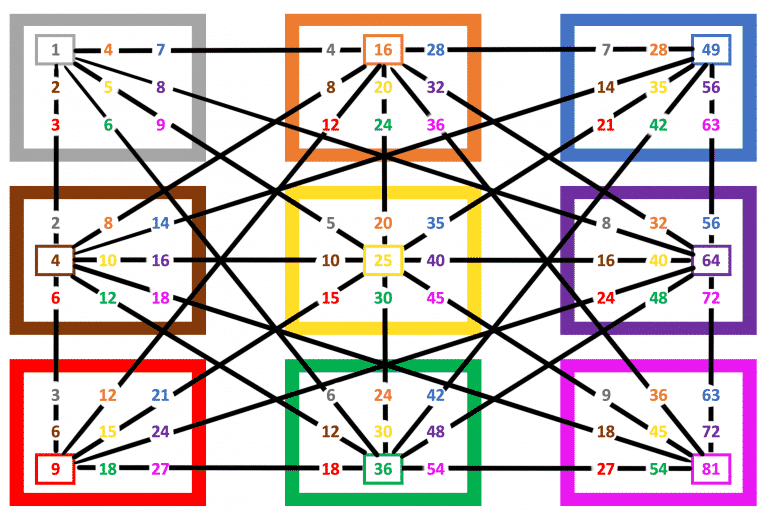
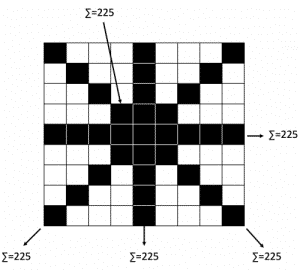
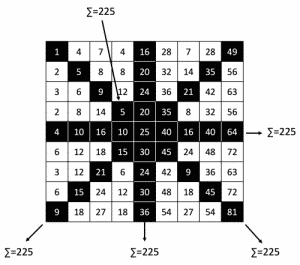
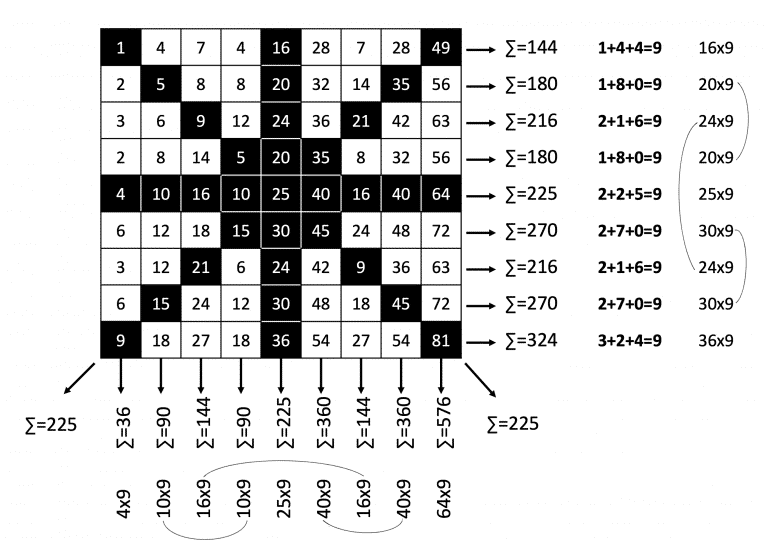
Central rows, central columns and diagonals
Furthermore, if we add up the values in the central row, the central column and the two diagonals, each add up to 225 which is a multiple of 9.
All values add up to 9 x 225 = 2025.
Note that the number in the centre of the square is 5² = 25.
∑ Values central rows, columns and diagonals = Centre value x 9 = 25 x 9 = 225
Interestingly, all other rows and columns also add up to values that are multiples of 9! Corresponding symmetry can also be noted.
∑ Values row = Value in the centre of that row x 9
∑ Values column = Value in the centre of that column x 9
∑ All values = 225 x 9
Although it is not a magic square, it has similar noteworthy properties.
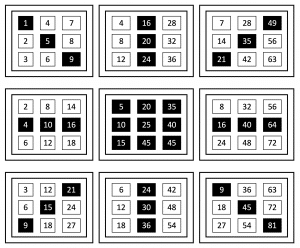
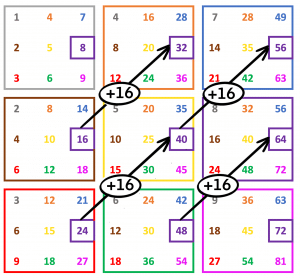
Relative relationships
Relative relationships exist for all adjacent numbers of the same colour in any fixed direction. Below images show the relative relationships of the purple numbers (x8).
Refer to directions in diagrams below:
→↑ plus 2×8=+16
→ plus 3×8=+24
→↓ plus 4×8=+32
Example - multiplier 8
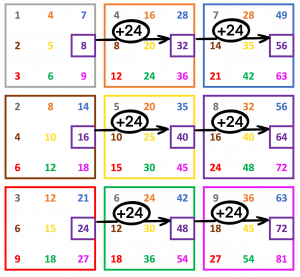
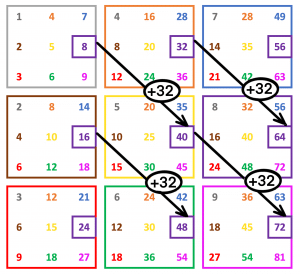
Similarly green numbers represent x6. Relationships of green numbers in the directions shown above:
→↑ plus 2×6=+12
→ plus 3×6=+18
→↓ plus 4×6=+24.
The same concept applies to any other colour or multiplier.
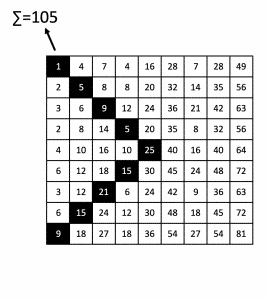
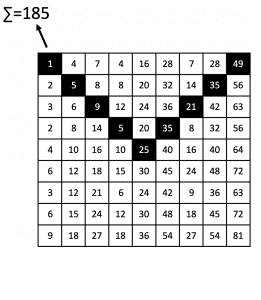
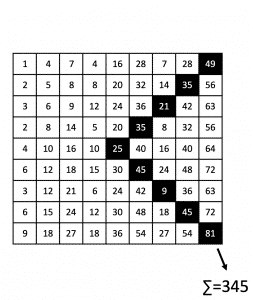
Another interesting observation - The following sums increase by 80
Number in the centre of the square = 5² = 25
25+80=105,
25+80+80=185,
25+80+80+80=265,
25+80+80+80+80=345

Note
Once we have memorised our tables up to 9×9, we have sufficient knowledge to multiply any two multiple digit numbers. It lays the foundation on which we can build 10,11 and 12. Also, multiplying by 10 and 11 is relatively easy whereas multiplying by 12 is double the 6 times table. An achievable goal!
Building a solid foundation is what is most important.
To set up the table of numbers, positions, colours and images, visit our page on how it works.
